Osteoporosis, a common condition in post-menopausal women, is defined as a systemic skeletal disease characterized by low bone mass and micro-architectural deterioration of bone tissue with a concomitant increase in bone fragility and fracture risk (1). It is recognized that osteoporosis is an important public health problem because of the large size of the affected population and because of the devastating impact of osteoporotic fractures on morbidity and mortality and on social costs. Health care expenditures in the United States attributable to osteoporotic fractures in 1995 were estimated at $13.8 billion (2) In addition to loss of bone mineral density, neuromuscular function and environmental hazards that influence the risk of fall, and the force of impact, as well as bone strength are important factors in determining fracture risk in the elderly (3) . Bone mineral density, geometry of bone, microarchitecture of bone and quality of the bone material are components that determine bone strength. On average, 70 - 80% of the variability in bone strength in vitro is determined by its density (4) . On an individual basis, density alone accounts for 10 – 90% of the variation in the strength of trabecular bone (5) . Preliminary data have shown that predicting trabecular bone strength can be greatly improved by including architectural parameters in the analysis (6) .

Micro-computed tomography (µCT) is an emerging technique to image and quantify bone in three dimensions. Early implementations of three-dimensional micro-tomography (7,8) have focused more on technical and methodological aspects while a more recent development (9) has emphasized practical aspects of micro-tomographic imaging. That system is based on a compact fan-beam type of tomograph, also referred to as desktop µCT, and has been used extensively for different research projects involving microstructural bone and biomaterials (10) . Since the introduction of this specific system, now successfully operating at the Orthopedic Biomechanics Laboratory, Beth Israel Deaconess Medical Center, there has been an increasing demand for micro-tomographic systems and applications throughout the world.

Dr. Müller is Associate Director of the Orthopedic
Biomechanics Laboratory at the Beth Israel Deaconess
Medical Center and Assistant Professor of Orthopaedic
Surgery at Harvard Medical School

Please address correspondence to:

Ralph Müller, PhD
Orthopedic Biomechanics Laboratory
Beth Israel Deaconess Medical Center and Harvard Medical 
School
330 Brookline Avenue, RN 115
Boston, MA 02215
rmueller@caregroup.harvard.edu

In this article, strategies for new approaches of bone modeling and simulation in the study and treatment of osteoporosis and age-related bone loss are presented. The focus is on the bioengineering and imaging aspects of osteoporosis research. With the introduction of desktop µCT, a new generation of imaging instruments has entered the arena allowing easy and relatively inexpensive access to the three-dimensional microstructure of bone, thereby giving bone researchers a powerful tool for the exploration of age-related bone loss and osteoporosis.

THREE-DIMENSIONAL MICROSTRUCTURAL IMAGING

Our desktop imaging system (µCT 20, Scanco Medical, Bassersdorf, Switzerland) was originally designed (9) for the non-destructive measurement and analysis of unprocessed surgical bone biopsies but can be used equally well for small animal whole bones and porous biomaterials. For each sample measured, a defined number of micro-tomographic slices are acquired depending on the size of the object assessed. Measurements are stored in three-dimensional image arrays. Total examination time ranges from minutes to hours depending on the number of slices acquired. After the measurement, bone tissue is segmented from marrow and solution with the help of a thresholding procedure (10) . For subsequent analysis, typically a volume of interest (VOI) of the originally measured data is selected including binarized bone tissue only.

MODELING METHODS

Surface Modeling

For the visualization of three-dimensional binary objects, the method described by Lorensen and Cline (1987) was followed. They developed an algorithm, called marching cubes (11) , which makes it possible to triangulate the surface of any given voxel array very quickly. The marching cubes algorithm is directly applicable to rastered three-dimensional data.

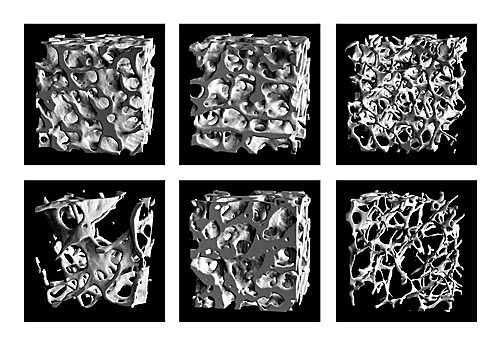Figure 1. Trabecular bone architecture of trabecular bone biopsies from differ-ent anatomical sites of a 37-year-old normal male (a-c) and an 84-year-old osteo-porotic male (d-f) respectively. The architecture as it is presented in normal iliac bone (a) resembles the one in the femoral head (b) and would be best described as a plate-like structure. The architecture in the lumbar spine (c) on the other side is distinctively different and would be referred to as a rod-like structure. In old age and osteoporosis, we notice a shift from plate- to rod-like structures in the iliac crest (d) whereas the femoral head (e) has not been affected for this specific individual. In the lumbar spine (f) the decrease in bone mass with age is represented as a complete resorption of structural elements leaving the struc-ture less well connected.

Using this simple divide-and-conquer approach, it is not only possible to obtain a three-dimensional polygonal surface represen-tation consisting exclusively of triangles, but also to smooth the surface effectively. To illustrate the capability of the surface reconstruction algorithm, a series of images are shown to illustrate the variability in architecture between different sites and age groups for a 37-year-old and an 84-year-old male, respectively (Figure 1). On a more microstructural level, µCT allows one to assess and visualize micro-callus formations (Figure 2), which typically form at locally overloaded places of the bone tissue. Although an indicator for relative instability of cancellous bone, its existence is not a negative process, but rather a physiological repair mechanism to renew old and brittle bone.

Figure 2. Two tra-becular microcallus formations in an iliac crest bone biop-sy of 84-year-old woman. The illustra-tion shows microcal-li at an early stage, where woven bone is the predominant type of tissue, which allows to rapidly sta-bilize the underlying microfracture.

Volume Modeling Since we are not only interested in surface properties of the bone architecture but also in the solid behavior, we would like to build bone models consisting of volumetric elements. Such models find application in the assessment of mechanical properties of bone, which is essential in the determination of the biomechanical competence of microstructural bone. In order to study nondestructively the influence of apparent den-sity and structural anisotropy on the mechanical properties, different microstructural models of cancellous bone have been introduced (12,13) . Most of these models are based on the assumption that different types of cancellous bone have identical tissue properties but varying microscopic structures. The findings from these studies demonstrate the need for more physiological models representing the trabecular microstructure in an accurate and detailed way. Müller and Rüegsegger (1995) extended the triangular surface representation generated by the marching cubes algorithm to a tetrahedral or hexahedral volume representation (14) . Like the original algorithm, the new algorithm, referred to as volumetric marching cubes (VOMAC), is applied on the three-dimensional discrete data set. The described technique allows the effective meshing of any digital structure for subsequent volumetric analysis. Although VOMAC was developed specifically for trabecular bone structures, the technique has recently been used (15) to successfully mesh other complex-shaped anatomical structures such as the human skull and brain as part of the Visible Human Project (Figure 3).

Figure 3. Four solid finite elements models of a human skull (33 x 46 x 46 voxels) as generated with traditional voxel-based hexahedron meshing (a) and with progressive model smoothing with one (b), two (c) and three (d) smooth-ing iterations, respectively. From the images it becomes clear that it is possible today to create very smooth and detailed volume models of bone structure using a fully automated approach. No user interaction is needed to generate these models.

SIMULATION METHODS

Non-Destructive Testing of Mechanical Bone Systems using Finite Element Analysis

The ultimate goal of any bone measurement in patients is to estimate bone strength. The relationship between structural indices of cancellous bone and the anisotropic mechanical properties is well documented (6,16) . An alternate approach to determine bone strength is to build models of bone using digital imaging and modeling techniques followed by a structural micro-finite element analysis (µCT). These models have shown that predicted tissue stresses and strains in bone specimens can differ considerably from those estimated from apparent level stresses and strains for the material as a continuum (17,18) . However, since the in situ loading conditions for these specimens are not exactly known, these models are not adequate for a realistic determination of stresses and strains in the bone tissue. For this reason, there is a need for full-scale models including the cortical shell and realistic boundary conditions to model the musculoskeletal interface resulting in an improved prediction of individual bone strength.

Recently, a large-scale microstructural model of an intact canine proximal femur was presented to determine the tissue loading conditions in trabeculae (19) . The objective of that study was to supply reasonable estimates of these quantities for the canine femur, and to compare predicted tissue stresses on the microstructural level to apparent stresses on the continuum level. A high-resolution computer reconstruction of the femur was made using a µCT scanner. This was converted to a large-scale FE model with 7.6 million elements and 9.1 million nodes. Using an iterative solver (17) , it was possible to solve this large problem in approximately 30 hours CPU time on a Cray C90 supercomputer. From a refined, local analysis in the center of the femoral head it was found that the predicted tissue loads were much higher than those estimated from the appar-ent values. However, for more than 97% of the tissue material, the tissue values were in the range of zero to four times the estimated apparent values. Ulrich et al. (1997) used the same technology to analyze an in vivo microstructural model of the distal radius measured with high-resolution 3D-QCT (20) . This was the first time that tissue-level stresses and strains were estimated in a living human subject.

Simulations of Age-Related Bone Loss and Osteoporosis Treatment

It is widely assumed that mechanical stresses and strains influence the remodeling process and subsequently, the structure and strength of the bone. The adaptive response of bone loading is generally referred to as Wolff's law (21) after the German anatomist who first called attention to it.

Traditionally, animal experiments have been employed to investigate bone response from load alterations or during the progress of age-related bone loss. Since the time scale of the remodeling process is on the order of months or years, com-putational modeling offers a unique approach to study long term processes without the inconveniences of animal experi-mentation. In a recent study, we investigated if changes in trabecular architecture as observed with age-related bone loss and osteoporosis can be predicted from a computer model that simulates bone resorption after hormone depletion over several decades. Our desktop µCT was used to measure two groups of seven trabecular bone specimens from pre- and post-menopausal women, respectively.

A novel algorithm was developed to simulate age-related bone loss for the specimens in the first group. The algorithm, referred to as simulated bone atrophy (SIBA), describes an iterative three-dimensional approach and is based directly on cel-lular bone remodeling with an underlying realistic time frame (22) . For our simulations, bone resorption and formation were in balance until the onset of menopause, set to be at the age of 50. After the onset of menopause, an imbalance in the cell activities was modeled resulting in a net bone loss. Using advanced visualization and animation tools as well as quantitative bone morphometry, the changes in bone architecture associated with the bone loss were monitored over an average time of 43 years until the age of 80 (Figure 4). By applying SIBA to the pre-menopausal specimens, it was possible to "age-match" these specimens with those from the post-menopausal group.

Additionally, the effects of bisphosphonates on the trabecular architecture were studied in two different treatment reg-mens by adjusting the values for the cellular activity levels. The first regimen consisted of a five-year block treatment beginning at the onset of menopause. The second regimen showed the effects of life-long bisphosphonate treatment at old age (20 years after the onset of menopause). Using quantitative bone morphometry and large-scale finite element analysis, changes in bone architecture and strength were monitored over approx-imately four decades. The results showed that changes in peri-menopause were most dramatic, and in fact, half the bone loss and half the loss in strength as assessed with microstructural finite element analysis occurred during that period (6 years). As a consequence, the five-year treatment block during peri-menopause was found to be most effective in preventing bone loss after menopause and resulted in improved architecture and strength (23) . It was concluded that peri-menopausal shortterm treatment of women at high risk might be a promising alternative to life-long treatment because of its cost effectiveness and the success in our simulations at preventing most of the bone loss and reduction in strength, thereby reducing the risk of fracture.

Figure 4. Simulated bone atrophy of an iliac crest and lumbar spine bone sample. The donors were 35 and 32 years of age, respectively, at the time of autopsy. Simulations were performed to model pre-, peri- and post-menopausal behavior of microstructural bone until the age of 80 years. The onset of menopause was defined at 50 years of age.