INTRODUCTION
Optimal management strategies for a number of conditions routinely encountered in orthopaedic practice remain controversial. The goal of evidence-based medicine is to integrate the best research evidence with clinical expertise and patient values.

Expected-value decision analysis is an important methodological tool in that it allows for the quantitative analysis of decision making under conditions of uncertainty. (1) The process of decision analysis involves structuring a decision question into a decision tree, determining outcome probabilities through a systematic literature review, and determining outcome utilities by surveying patients. Decision analysis can then be used to determine the optimal decision and to examine how decision making changes with varying outcome probabilities and utilities. (1)

Recently, we have applied expected-value decision analysis to the controversy surrounding management of acute Achilles tendon rupture - operative repair versus non-operative cast immobilization - and to the uncertainty surrounding management of the unaffected contralateral hip after a unilateral slipped capital femoral epiphysis (SCFE) - watchful waiting versus prophylactic pinning. (2, 3) This paper will use examples from both of these studies to review the techniques and implications of expected-value decision analysis.

STEP 1: STRUCTURING THE DECISION PROBLEM
The first step in any decision analysis is to construct a decision tree to structure the decision problem. The decision tree must represent the decision, any uncertain events, and all of the possible outcomes. With acute Achilles tendon rupture, the decision tree consists of one decision point (decision node) of operative vs. non-operative management, two uncertain points (chance nodes), and ten possible outcomes (terminal nodes) (Figure 1). Per convention, utility data is placed to the right of the terminal nodes and probability data under the terminal nodes.

STEP 2: DETERMINING OUTCOME PROBABILITIES
Outcome probability estimates are determined by systematic literature review of best-available evidence. This data is represented on the decision tree beneath each terminal node (Figure 1).

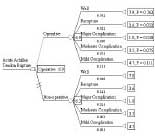Figure 1: Decision Tree for Acute Achilles Tendon Rupture. Decision nodes are represented by o, chance nodes are represented by O, and the terminal nodes are represented by Þ. Expected value for each decision arm is listed to the right of the chance nodes (O). Optimal decision strategy and its expected value are listed to the right of the decision node (o)

STEP 3: DETERMINING OUTCOME UTILITIES
Outcome utilities are meant to represent the value of each scenario to the decision-maker. There are a number of techniques for determining utility. The one we have recently utilized is a visual-analog scale questionnaire posing scenarios for the different outcomes and asking subjects to rate these outcomes on a 0-10 scale, where 0 represents the worst possible medical outcome and 10 represents the best (Figure 2). These utilities are then added to the decision tree to the right of the terminal nodes (Figure 1).

STEP 4: FOLD BACK ANALYSIS
Fold back analysis of the decision tree describes the process by which the expected value of each decision is calculated. 1 This is done by weighing the utility of each outcome with its probability. For example, the expected value of operative repair of Achilles tendon rupture is calculated using the established utilities and probabilities as follows: EXPECTED VALUE OF OPERATIVE REPAIR =
(7.90 * 0.762) + (2.60 * 0.22) + (1.00 * 0.030) + (3.50 * 0.075) + (4.70 * 0.111) = 6.9 The same fold back calculation can be performed for the non-operative branch of the decision tree, and yields an expected value of 6.30. Each expected value is represented in a box at the corresponding chance node (Figure 1). Rational decision-making favors the decision path with the highest expected value.

STEP 5: SENSITIVITY ANALYSIS
Sensitivity analysis is used to determine how decision making is affected by variations in probability or utility values. 1 In the unilateral SCFE decision analysis, the probability of a late contralateral slip in the previously normal hip was a major driving factor. 3 Therefore, it is illuminating to examine the sensitivity analysis performed for this variable (Figure 3). Sensitivity analysis shows that prophylactic pinning is favored when the probability of a late second slip exceeds 38%. Therefore, the surgeon can tailor the decision-making process to patients deemed high risk for a second slip and pin prophylactically when appropriate.

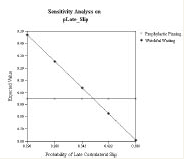Figure 3: One-Way Sensitivity Analysis: Probability of Late Contralateral Slip. The probability of late contralateral slip is varied on the x-axis. The lines represent the expected value for the prophylactic pinning and watchful waiting decisions.

SUMMARY
In orthopaedic practice the surgeon is commonly confronted with difficult decisions between various treatment modalities, each with defined advantages and disadvantages. In these situations, expected-value decision analysis is an important methodological tool that allows for the quantitative analysis of decision making under conditions of uncertainty. (1) The process involves the creation of a decision tree to structure the decision problem, fold back analysis to calculate expected value and determine the optimal decision-making strategy, and sensitivity analysis to determine the effect on decision making of varying outcome probabilities and utilities.

In conclusion, expected-value decision analysis may help us better understand the decision process that physicians and patients face in orthopaedic surgery. The optimal decision for any specific patient depends not only on the probabilities of the various outcomes, but also on the utility of these outcomes for the patient. Hence, there may not be one right therapeutic answer for all patients, but rather the patient’s preferences should be explored.

Julius Bishop, BA is a Harvard Medical Student.

Mininder Kocher, MD, MPH is an Instructor in Orthopedic Surgery Harvard Medical School and is Director of Orthopedic Institute for Clincal Effectiveness, Children’s Hospital.

Address Correspondence to:
Mininder Kocher, MD,
MPH Children’s Hospital
300 Longwood Avenue
Boston, MA 02115
phone: (617) 355-6617
fax: (617) 739-3338
mininder.kocher@tch.harvard.edu

Print Manuscript   •  View References  •  Download PDF version   •  Close window